Image Restoration with Mean-Reverting Stochastic Differential Equations
Abstract
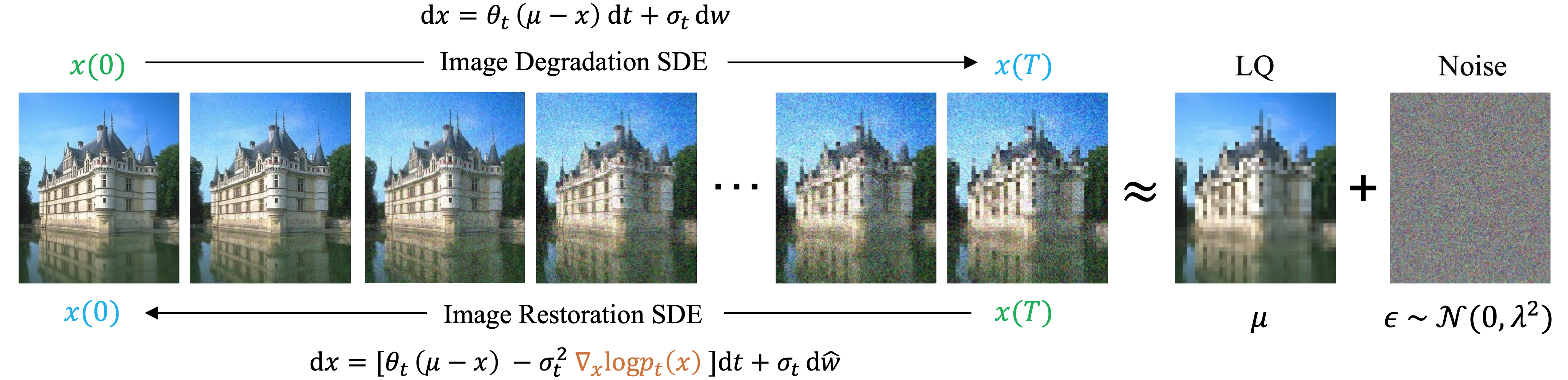
This paper presents a stochastic differential equation (SDE) approach for general-purpose image restoration. The key construction consists in a mean-reverting SDE that transforms a high-quality image into a degraded counterpart as a mean state with fixed Gaussian noise. Then, by simulating the corresponding reverse-time SDE, we are able to restore the origin of the low-quality image without relying on any task-specific prior knowledge. Crucially, the proposed mean-reverting SDE has a closed-form solution, allowing us to compute the ground truth time-dependent score and learn it with a neural network. Moreover, we propose a maximum likelihood objective to learn an optimal reverse trajectory which stabilizes the training and improves the restoration results. In the experiments, we show that our proposed method achieves highly competitive performance in quantitative comparisons on image deraining, deblurring, and denoising, setting a new state-of-the-art on two deraining datasets. Finally, the general applicability of our approach is further demonstrated via qualitative results on image super-resolution, inpainting, and dehazing.